고정 헤더 영역
상세 컨텐츠
본문

음성 신호는 연속적으로 변화하는 패턴 / 파형이다. 그리하여 연속적 신호를 샘플링하여야 컴퓨터를 통하여 활용할 수 있다.b
(b)의 그래프를 보게 되면 점이 계속해서 찍혀있고 y축에 평행한 선들이 그어져 있는 것을 확인할 수 있다. 이처럼 연속적인 신호를 이산적 데이터로 샘플링 한 것을 알 수 있다.

Nyquist's Sampling Theory (나이퀴스트 샘플링 이론)
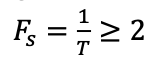
해당 식으로 확인 가능한 것은, 신호를 정확히 복원하기 위해서는 최고 주파수의 최소 2배 이상의 속도로 샘플링해야 한다는 것이다.
그 이유는, 2배 이상으로 샘플링하지 않으면 aliasing 이라는 현상이 발생한다.
해당 현상이 일어나면, 신호 왜곡(고주파 성분->저주파 성분으로 해석), 정보 손실(일부 주파수 성분이 손실), 겹침 현상 (주파수 스펙트럼에서 신호의 복사본들이 서로 겹치면서 원래 신호의 스펙트럼 구분 불가) 등의 문제가 일어날 수 있다.

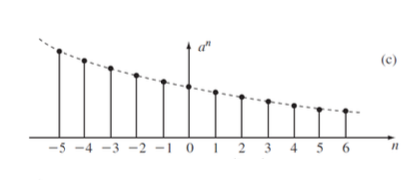
Unit Impulse(단위 임펄스), Unit step(단위 스텝)
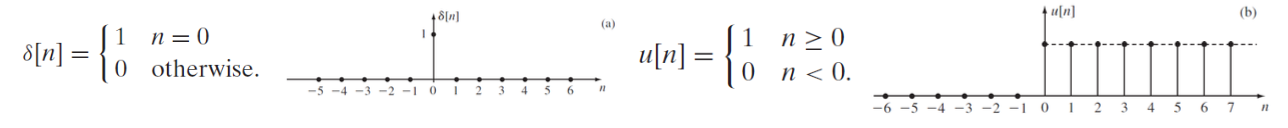
Unit Impulse는 n=0에서만 1이고 다른 모든 지점에서 0인 Impulse 함수를 보여줌
Unit step은 (n>=0)에서 1이고, n<0일때 0이다.

해당 그래프는
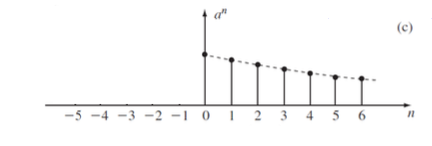
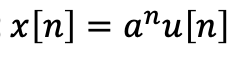
-> 이 부분에 대한 이해가 안됐다. Impulse 라는 것은 뭐고 단위 Impulse는 무엇인지
기본적인 Impulse라는 것은 특정한 상황에서만 1이라는 값을 갖는 신호나 함수를 의미한다고 한다.
step function은 기본적으로 계단 느낌 갖는 저 함수를 의미한다고 받아들였다. 그럼 이 두 가지 단위 벡터처럼 기본적인 형태를 의미한다고 가정하면, applying 된 저것의 사용 이유와 의미를 찾아보면 시스템 분석의 기초가 된다고 한다. (음...?)
(Unit Impulse를 Input으로 하면 output Impulse가 나오게 되고, 해당 Impuls로 시스템의 모든 특성을 알 수 있다.)
Linear Time Invariant 시스템에서는 Impulse 응답을 알면 어떤 입력에 대해서도 출력을 예측할 수 있다고 한다.
해당 방법을 통하면 복잡한 신호를 단순한 기본 요소들의 조합으로 표현 가능하다.
또한 Convolution과 같은 연산에서 수학적으로 다루기 쉽고, Unit step function은 신호가 특정 시점부터 시작되는 경우를 모델링하는데좋다.

연속 데이터를 이산 데이터로 바꾼 형태
Block Diagram Representation (블록 다이어그램 표현)

1. 신호 처리 중 변환
- 신호 처리 과정에서 입력 신호가 어떤 변환을 거쳐 출력 신호로 바뀜
2. 블록 다이어그램 표현
- 이러한 변환 과정을 시각적으로 표현하기 위해 블록 다이어그램 사용
- (a) (b) 동일한 시스템을 표현하는 두 가지 방식의 블록 다이어그램
- 두 다이어그램 모두 입력 신호 x[n]이 변환 T[]를 통과하여 출력 신호 y[n] = T[x[n]]이 되는 과정을 보여줌
3. 시간 변화 매개변수 추정
- 많은 시스템들을 샘플링된 음성 파형에서 시간에 따라 변하는 매개변수들을 추정하도록 설계되어 있음.
선형 시불변 (LinearTime-Invariant, LTI) 신호
1. 음성처리에서 매우 유용하게 사용됨
2. 선형성
- 선형 시스템에서는 입력 x[n]이 출력 y[n]을 생성할 때, 입력 ax[n] + bx'[n]은 출력 ay[n]+by'[n]을 생성한다.
- 신호의 선형 조합(가중합)이 출력의 선형 조합과 동일하다는 의미
3. 시불변성
- 시불변 시스템에서는 입력 x[n]이 출력 y[n]을 생성할 때, 시간 지연된 입력 x[n-T]는 동일하게 시간 지연된 출력 y[n-T]를 생성합니다.
- 시스템의 특성은 시간에 따라 변하지 않는다.
4. 임펄스 응답을 통한 완전 특성화:
- LTI 시스템은 단위 임펄스 입력에 대한 응답 h[n]으로 완전히 특성화될 수 있음.
- 임의의 입력 x[n]에 대한 출력 y[n]은 다음 식으로 convolution 연산으로 계산됨

LTI(선형 시불변) 시스템의 중요한 특성에 관해 설명
1. 인과성 (causality)
- 이산 시간 LTI 시스템이 인과적이라는 것은 현재 출력값이 현재와 과거의 입력값에만 의존
- 미래의 입력값은 현재 출력에 영향을 미치지 않음
- 충분조건 h[n]=0 (모든 n<0에 대해)
- 이는 임펄스 응답 h[n]이 n이 음수인 구간에서 모두 0이어야 한다는 조건
2. 안정성 (stability)
- 시스템이 BIBO(bounded input, bounded output) 안정적이라는 것은 모든 유한 입력에 대해 출력도 유한하다는 의미
- 충분조건 ||h[n]||₁ = Σ(n=-∞ to ∞) |h[n]| < ∞
- 임펄스 응답의 절대값 합이 유한해야 한다는 조건이다.
-> 인과성은 실시간 시스템에서 필수적, 안정성은 제어 가능하게 동작하기 위해서 필요함. 불안정한 시스템은 유한한 입력에도 출력이 발산할 수 있다.
Transforms of Signals and Systems

1.신호를 변환하는 이유
- 신호를 다른 도메인에서 이해하기 위함
- 스펙트럼 성분별 분석을 가능하게 한다.
2. 도메인 변환 과정
- 시간 도메인(time domain)
-- 입력 신호 x(t)가 시스템 h(t)를 통과하여 y(t) = h(t) * x(t)를 생성
- 주파수 도메인 (frequency domain)
-- 라플라스 변환 (laplace transform)을 통해 시간 도메인의 신호와 시스템을 주파수 도메인으로 변환함
-- 입력 신호 X(s), 시스템 H(s), 출력 Y(s) = H(s) · X(s)
-- 주파수 도메인에서는 컨볼루션 연산이 단순한 곱셈으로 바뀐다.
-- 역변환(Inverse Laplace)을 통해 다시 시간 도메인으로 돌아갈 수 있다.
-> 변환의 핵심 이점 : 시간 도메인의 컨볼루션 연산이 주파수 도메인에서는 단순한 곱셈으로 처리됨(단순화, 음성 신호의 특정 주파수 성분을 강화하거나 제거하는 필터링 작업이 훨씬 직관적이고 효울적으로 수행될 수 있음)
푸리에 변환 (Fourier Transform) -> 이 부분 알아야 함
1. Continuous version

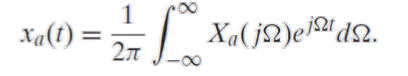
Ω = 2πF (F는 주기적 속성인 주파수를 나타냄)
2. Discrete version

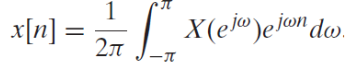
푸리에 변환은 신호를 주파수(스펙트럼) 도메인으로 변환한다.
시간 도메인 신호를 주파수 성분들로 분해하여 다른 관점에서 분석할 수 있게 해줌
(음성 신호의 경우, 푸리에 변환을 통해 다양한 주파수 성분(저음, 고음)을 분석하고 조작할 수 있다.)
+ 푸리에 변환에 대해서 좀 더 살펴보자
해당 순방향과 역방향 식에 대해서 째려보다 보면 e^(i)의 형태가 오일러 공식과 닮았다는 것을 알 수 있다.

기본 원리는 모든 주기적 신호는 다양한 주파수의 사인파와 코사인파의 합으로 표현할 수 있다는 것이다.
1. 복수지수함수 표현 : 주파수의 사인파와 코사인파의 합을 e^(iωt) 이러한 식으로 좀 더 간단하게 나타내었다.
2. 회전하는 복소수 벡터 : 복소평면에서 e^(iωt) 단위 원을 따라 회전하는 벡터로 볼 수 있다. 회전 속도는 w에 비례한다.
3. 신호 분석 : 신호 x(t)에 e^(-iwt)를 곱하고 적분하면, 해당 주파수 w에서 신호의 성분을 추출할 수 있다.
Z-Transform


Z변환을 사용하는 이유는 Z 변환에서 z = e^(jw)로 대체하면 이산 푸리에 변환(DTFT)이 된다.
즉 단위 원 (|z| = 1)위에서의 Z-변환이 DTFT이다.
무한 멱급수: Z-변환은 z^(-1)의 무한 멱급수로 볼 수 있으며, x[n]은 이 멱급수의 계수 역할을 합니다.
- 이는 라플라스 변환이 연속 신호에 대한 것이라면, Z-변환은 이산 신호에 대한 변환이라고 볼 수 있습니다.
수렴: 일반적으로 Z-변환 X(z)는 다음 조건에서 수렴합니다:
- Σ(n=-∞ to ∞) |x[n]||z^(-n)| < ∞
- 즉, 이 무한 합이 유한한 값을 가질 때 수렴합니다.
수렴 영역(ROC): 수렴 영역은 Z-변환이 수렴하는 z값의 범위를 나타냅니다.
- R₁ < |z| < R₂ 형태로 표현됩니다.
- 이는 복소 평면에서 원환(annular) 형태의 영역을 의미합니다.
Z-변환과 이산 시간 푸리에 변환 (Discrete time fourier Transform, DTFT) # (∮ : 폐곡선 적분)

왼 : Z-변환, Inverse Z-변환
오른: DTFT, Inverse DTFT
관계 : z = e^(jw)로 설정 시, z-변환과 DTFT는 동일
이는 복소 평면에서 z가 단위원을 따라 움직일 때 (|z| = 1) Z-변환이 DTFT와 일치함을 의미합니다.
DTFT가 존재하기 위해서는 신호 x[n]이 절대 합산 가능(absolutely summable)해야 합니다: Σ(n=-∞ to ∞) |x[n]| < ∞
Z-변환의 수렴 영역이 단위원을 포함해야 함을 의미함.

DTFT의 주기성: 이산 시간 푸리에 변환 X(e^(jω))는 ω에 대해 주기적이며, 그 주기는 2π입니다.
- 이것은 X(e^(j(ω+2π))) = X(e^(jω))
- 즉, 주파수 영역에서 2π만큼 이동하면 같은 값이 반복
기하학적으로 w를 0~2π까지 변화시키면 단위원을 한바퀴 돌게 됨. -> 주파수가 2π 증가하면 같은 복소수 값으로 돌아오는 것을 의미함.
DTFT
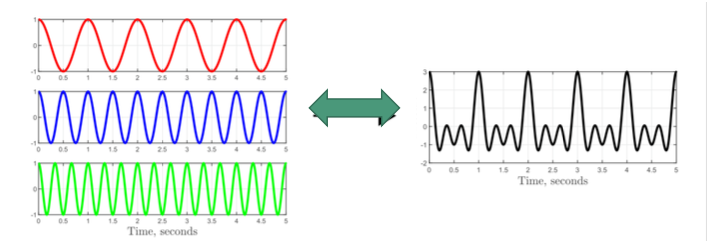
주기적 시퀀스의 표현
- 주기 N을 가진 이산 시퀀스 x̃[n] = x̃[n + N]는 사인파들의 이산적인 합으로 표현될 수 있다.
- 그래프는 다른 주파수를 가진 다양한 사인파가 어떻게 합쳐져서 더 복잡한 주기적 신호를 만드는 지 보여줌
주파수 성분
- 각 성분은 (2πk/N)의 라디안 주파수. 여기서 k는 0, 1, 2, ..., N-1의 값
- N은 주기적 시퀀스의 주기
- 이는 N개의 서로 다른 주파수 성분이 있음을 의미.
이산 푸리에 변환



-> 해당 파트로 알 수 있는 것은, 주기적 신호를 완전히 파악하기 위해선 단 하나의 주기만 알면 충분하다.
한 주기의 정보만으로도 전체 무한 신호를 재구성할 수 있다.
"now we don't have Tilda; we don't need periodicity and deterministic restriction anymore"라는 문구는 DFT가 주기적 신호뿐만 아니라 임의의 유한 길이 신호에도 적용될 수 있음을 의미
DTFT(연속적인 주파수 영역) vs DFT (이산적인 주파수 영역)
DFT : 암시적 주기성
-> 기본적으로 신호의 주기성을 암시적으로 전제
-> 유한 길이 신호 분석 시, 이 신호가 주기적 반복된다 가정함
길이 L인 DTFT

-> X(e^(jω)) = Σ(n=0 to L-1) x[n]e^(-jωn)
DTFT의 샘플링
: DTFT X(e^(jω))가 0 ≤ ω < 2π 범위에서 알려져 있다고 가정하면,
특정 주파수 ω_k = (2πk/N)에서 X(e^(jω))를 샘플링(평가) 가능 (0<= k <= N-1)
DFT와의 관계 : 샘플링된 값들은 DFT 계수를 형성

-> X_N[k] = X(e^(j(2π/N)k)) = Σ(n=0 to L-1) x[n]e^(-j(2π/N)kn)
-> 길이 L인 시퀀스의 N point DFT를 정의
+ 다음 ppt 장
: 시퀀스의 특성
-> n-sample finite length sequence => n개의 샘플을 가진 유한 길이 시퀀스
L>=N이면, x[n]은 0으로 패딩 (제로 패딩)
inverse DFT
-> 이 식을 통해서 주파수 영역의 데이터 x_N[k]로 부터 시간 영역의 신호 x_N[n]을 복원할 수 있음
DTFT의 샘플링과 관련된 시간 영역 Aliasing

시퀀스의 길이(L)가 DFT 포인트 수(N)보다 큰 경우
신호 길이(L)가 DFT 포인트 수(N)보다 크면, 주기적으로 반복되는 신호의 일부가 서로 중첩되어 왜곡이 발생함.
(b)의 경우 주파수 영역에서 발생하는 알리아싱 효과를 보여줌.
=> 마지막 부분 추가 공부 필요(DTFT DFT 사이의 관계까지는 이해가 가는데 마지막 부분에 대해서 잘 이해가 가지 않음)
'음성인식' 카테고리의 다른 글
| [프로젝트] 음성인식 프로젝트 #1 딥러닝 모델 (0) | 2025.04.17 |
|---|---|
| [프로젝트] .gitignore과 requirement.txt 추가 및 docker 연동 (+로드 밸런싱 신기하다) (0) | 2025.04.16 |
| [음성인식] 3주차 강의 (월요일 수업) #3 Sampling (0) | 2025.03.21 |
| [음성인식] 3주차 강의(월요일 수업) #2 Filter (0) | 2025.03.21 |
| [음성인식] 3주차 정리(월요일 수업) #1 푸리에 변환 및 여러가지 (0) | 2025.03.20 |




