[데이터 사이언스] 6. 예측 모델링 - 정보이론

정보이론과 엔트로피

- 2차 세계 대전 당시 클로드 새넌에 의해 발전

- 불완전한 통신 채널을 통해 정보를 전송 시, 정보 전송의 효율을 최대화하기 위한 이론(엔트로피)을 개발

 

정보량 (Quantity of information, I)

- 한 사건에서 기대되는 정보량을 어떻게 나타낼 수 있을 지를 생각

- 정보량을 수량화하기 위하여 확률(P)과 정보량(I)을 다음의 두 확률 조건의 관점에서 살펴봄

 

조건 1 : 중요성 (significance)

어떤 사건이 일어날 가능성이 작으면 작을수록 그 사건은 더 많은 정보를 지닌다

조건 2 : 가법성 (additivity)

만일 x_1, x_2가 독립적인 사건이라면 다음을 만족해야 한다

정보량

- 중요성 조건은 어떤 사건의 확률이 높을수록, 이 사건으로부터 알려지는 정보량은 적어짐을 의미

- 정보량은 확률 값을 역으로 취해서 얻을 수 있음

정보량과 확률의 관점

 

해당 방식으로는 가법성의 조건이 충족되지 못함을 보인다. (곱이 덧셈으로 가능해야함)

 

핵심 문제 : 두 독립 사건의 확률은 곱셈 관계이지만, 결합된 정보량은 덧셈 관계로 표현되어야 함

따라서 정보의 가법성을 만족시키기 위해 곱이 아닌 더하기 구조를 만드는 로그 함수를 도입하게 됨

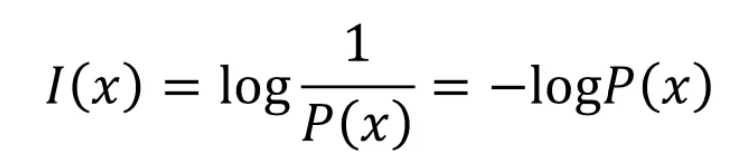
엔트로피 (Entropy)

- 확률 변수 x의 표본 공간에서 나타나는 모든 사건들의 정보량의 평균적인 기대값을 엔트로피 H로 표시

- 일반적인 엔트로피는 어떤 확률 변수가 지니는 평균적인 불확실성(Unvertainty) 혹은 무질서를 측정하는데 이용됨

엔트로피는 한 확률변수에서 나타나는 개별적인 사건의 확률과 그 정보량을 곱하고, 이를 모두 더해서 얻어짐

-> 나올 수 있는 모든 정보와 그 확률에 대한 것이 더해짐